 Imaginez : vous venez d’acheter la voiture de vos rêves. Les premières semaines, chaque trajet est une petite fête intérieure. Mais des mois plus tard… c’est juste “la voiture”. La magie a disparu.. Ce phénomène porte un nom : l’habituation hédonique. Notre cerveau s’habitue aux plaisirs, jusqu’à les rendre presque invisibles. Dans cet épisode, détaillons ce comportement fascinant et découvrons des techniques pour en limiter l’effet. C’est parti.
Imaginez : vous venez d’acheter la voiture de vos rêves. Les premières semaines, chaque trajet est une petite fête intérieure. Mais des mois plus tard… c’est juste “la voiture”. La magie a disparu.. Ce phénomène porte un nom : l’habituation hédonique. Notre cerveau s’habitue aux plaisirs, jusqu’à les rendre presque invisibles. Dans cet épisode, détaillons ce comportement fascinant et découvrons des techniques pour en limiter l’effet. C’est parti.
Version vidéo
https://youtu.be/c0nkziImi-Q
Version audio
https://open.spotify.com/episode/5e4Se0UZHDbIifncWv3rz8?si=GKLwShGrSrqvh03Y4RGGKQ
L’habituation hédonique : pourquoi nos joies s’éteignent avec le temps (et comment y remédier)
Qu’est-ce que l’habituation hédonique ?
L’habituation hédonique est la tendance qu’a notre cerveau à s’habituer aux événements positifs, si bien que leur impact émotionnel diminue avec le temps. Que ce soit un gain financier, une relation amoureuse, un nouvel objet ou même une réussite personnelle, l’excitation initiale finit par retomber.
Voici quelques exemples concrets :
- L’achat d’une montre haut de gamme, un sac de créateur ou une paire en édition limitée suscitent un fort plaisir initial… qui s’évapore une fois que l’objet fait partie de notre quotidien.
- Juste après l’achat d’un nouveau parfum, l’odeur est très marquée les premiers jours, puis l’intensité diminue jusqu’à ce qu’on ne le remarque même plus.
- Durant les premières semaines en couple, tout est intense et euphorique. Avec le temps, la routine s’installe, et le cerveau s’habitue à la présence de l’autre.
- Lorsqu’on démarre un nouveau jeu vidéo, on est souvent très excité, mais au bout d’une dizaine de partie la joie s’atténue.
Les études confirment ce phénomène. En 1971, les psychologues Philip Brickman et Donald Campbell démontrent que les gagnants du loto retrouvent un niveau de bonheur proche de celui de la population générale après un an. En 2007, Richard Lucas observe que le niveau de satisfaction retombe progressivement à la moyenne après un mariage.
- Sources : Brickman, P., & Campbell, D. T. (1971). Hedonic relativism and planning the good society : https://archive.org/details/adaptationlevelt0000unse_x7d9/page/286/mode/2up
- Lucas, R. E. (2007). Adaptation and the Set-Point Model of Subjective Well-Being: Does Happiness Change After Major Life Events? : https://journals.sagepub.com/doi/abs/10.1111/j.1467-8721.2007.00479.x
Au bout du compte, on constate cette même mécanique partout. Notre cerveau s’habitue aux plaisirs, jusqu’à les rendre presque invisibles.
5 pistes pour limiter l’habituation hédonique
Comment ralentir le processus de l’habituation hédonique ? Voici quelques pistes :
- Pratiquer la gratitude. Par exemple, en prenant l’habitude de noter tous les jours 3 choses positives qui nous sont arrivées afin de prolonger leur impact.
- Espacer les plaisirs : un carré de chocolat par jour vaut mieux qu’une tablette d’un coup.
- Rendre les plaisirs rares : limiter volontairement l’accès à certaines choses qu’on aime afin d’amplifier leur valeur.
- Se créer des rituels, en sacralisant certains plaisirs à un moment.
- Investir dans les expériences plutôt que dans les objets, car les souvenirs se réactivent plus facilement.
Conclusion
L’habituation hédonique est la tendance qu’a notre cerveau à s’habituer aux événements positifs, si bien que leur impact émotionnel diminue avec le temps. Cet inévitable processus est un puissant moteur puisque la volonté de ressentir à nouveau de la joie, nous pousse à partir en quête de nouveaux défis. Cette mécanique va aussi de pair avec une vérité simple : la joie est éphémère et n’est pas seulement dans l’acquisition, mais dans la façon dont on entretient la relation avec ce plaisir.
Sources
- Brickman, P., & Campbell, D. T. (1971). Hedonic relativism and planning the good society : https://archive.org/details/adaptationlevelt0000unse_x7d9/page/286/mode/2up
- Lucas, R. E. (2007). Adaptation and the Set-Point Model of Subjective Well-Being: Does Happiness Change After Major Life Events? : https://journals.sagepub.com/doi/abs/10.1111/j.1467-8721.2007.00479.x
- Frederick, S., & Loewenstein, G. (1999). Hedonic adaptation. https://www.cmu.edu/dietrich/sds/docs/loewenstein/HedonicAdaptation.pdf
__________________________
Retourner à la page d’accueil du projet P07
__________________________


 Et si le simple fait d’écrire nos pensées sur papier pouvait améliorer notre mémoire, booster notre concentration, et nous aider à résoudre nos problèmes ? Dans cet épisode, explorons un geste aussi banal que puissant : prendre des notes à la main. C’est parti !
Et si le simple fait d’écrire nos pensées sur papier pouvait améliorer notre mémoire, booster notre concentration, et nous aider à résoudre nos problèmes ? Dans cet épisode, explorons un geste aussi banal que puissant : prendre des notes à la main. C’est parti ! Imaginez que vous soyez arrêtés avec un complice pour un délit. On vous demande de passer aux aveux. Le procureur vous présente plusieurs options :
Imaginez que vous soyez arrêtés avec un complice pour un délit. On vous demande de passer aux aveux. Le procureur vous présente plusieurs options :  Avez-vous déjà eu l’impression qu’on déformait vos propos juste pour vous contredire ? Ou à l’inverse, avez-vous déjà rencontré quelqu’un capable de reformuler parfaitement vos arguments avant d’y répondre avec finesse ? Ces deux manières diamétralement opposées de débattre portent des noms : l’homme de paille et l’homme de fer.
Avez-vous déjà eu l’impression qu’on déformait vos propos juste pour vous contredire ? Ou à l’inverse, avez-vous déjà rencontré quelqu’un capable de reformuler parfaitement vos arguments avant d’y répondre avec finesse ? Ces deux manières diamétralement opposées de débattre portent des noms : l’homme de paille et l’homme de fer.  Saviez-vous qu’il est possible de détecter les fraudes comptables, vérifier les résultats électoraux ou encore évaluer la fiabilité d’une source grâce aux mathématiques ? Cette performance s’appuie sur une curiosité statistique fascinante : la loi de Benford. Dans cet épisode, découvrons ce concept étonnant et les applications concrètes que nous pouvons en tirer. C’est parti !
Saviez-vous qu’il est possible de détecter les fraudes comptables, vérifier les résultats électoraux ou encore évaluer la fiabilité d’une source grâce aux mathématiques ? Cette performance s’appuie sur une curiosité statistique fascinante : la loi de Benford. Dans cet épisode, découvrons ce concept étonnant et les applications concrètes que nous pouvons en tirer. C’est parti !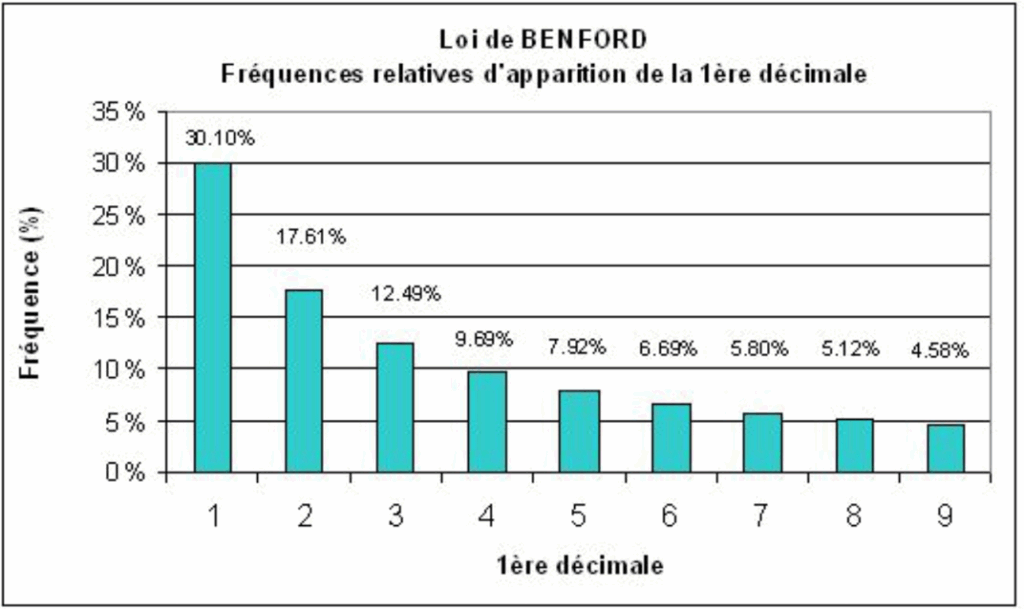

 Connaissez-vous l’histoire des cobras de Delhi ? Au 19e siècle, Delhi fait face à une invasion de cobras venimeux. Pour résoudre le problème, les autorités instaurent une prime pour chaque cobra mort rapporté. D’abord efficace, la mesure entraîne ensuite des dérives : des habitants élèvent des cobras pour profiter de la récompense. En découvrant la supercherie, l’administration supprime le programme. Furieux, les éleveurs relâchent leurs serpents dans les rues. Résultat : la situation empire car la population de cobras augmente drastiquement. Cette histoire vraie illustre un phénomène bien connu en économie et en sciences sociales que l’on nomme l’effet Cobra. Ce terme désigne une situation où une tentative de solution à un problème entraîne des conséquences involontaires qui empirent la situation initiale. C’est parti pour quelques explications !
Connaissez-vous l’histoire des cobras de Delhi ? Au 19e siècle, Delhi fait face à une invasion de cobras venimeux. Pour résoudre le problème, les autorités instaurent une prime pour chaque cobra mort rapporté. D’abord efficace, la mesure entraîne ensuite des dérives : des habitants élèvent des cobras pour profiter de la récompense. En découvrant la supercherie, l’administration supprime le programme. Furieux, les éleveurs relâchent leurs serpents dans les rues. Résultat : la situation empire car la population de cobras augmente drastiquement. Cette histoire vraie illustre un phénomène bien connu en économie et en sciences sociales que l’on nomme l’effet Cobra. Ce terme désigne une situation où une tentative de solution à un problème entraîne des conséquences involontaires qui empirent la situation initiale. C’est parti pour quelques explications ! Si l’on vous donnait un an pour gagner un million d’euros, pensez-vous y arriver ? Probablement pas. Par contre, si maintenant on vous demandait d’atteindre le million dans l’année sous peine de perdre tous vos proches à la fin du délai. Dans ce cas, davantage de personnes s’estiment en mesure d’atteindre l’objectif. Paradoxalement, la tâche et son délai restent identiques. La seule différence est la source de motivation. Cet exemple met en lumière une question fascinante : qu’est-ce qui nous pousse à agir ? Dans cet épisode, nous allons explorer 3 types de motivation et expliquer comment nous pouvons les utiliser pour améliorer notre quotidien. C’est parti !
Si l’on vous donnait un an pour gagner un million d’euros, pensez-vous y arriver ? Probablement pas. Par contre, si maintenant on vous demandait d’atteindre le million dans l’année sous peine de perdre tous vos proches à la fin du délai. Dans ce cas, davantage de personnes s’estiment en mesure d’atteindre l’objectif. Paradoxalement, la tâche et son délai restent identiques. La seule différence est la source de motivation. Cet exemple met en lumière une question fascinante : qu’est-ce qui nous pousse à agir ? Dans cet épisode, nous allons explorer 3 types de motivation et expliquer comment nous pouvons les utiliser pour améliorer notre quotidien. C’est parti !  Comment prouve-t-on que la Terre est ronde ? Comment vérifier la validité d’une théorie scientifique ? Dans un autre registre, comment expliquer qu’à partir d’une même réalité, les individus aboutissent à des opinions différentes ? Par exemple, certaines expliquent que le réchauffement climatique est causé par les activités humaines alors que d’autres considèrent que ces changements sont dus à des cycles naturels. Dans cet épisode, intéressons-nous à la manière dont nous raisonnons. Découvrons plus précisément le raisonnement inductif et le raisonnement déductif. C’est parti !
Comment prouve-t-on que la Terre est ronde ? Comment vérifier la validité d’une théorie scientifique ? Dans un autre registre, comment expliquer qu’à partir d’une même réalité, les individus aboutissent à des opinions différentes ? Par exemple, certaines expliquent que le réchauffement climatique est causé par les activités humaines alors que d’autres considèrent que ces changements sont dus à des cycles naturels. Dans cet épisode, intéressons-nous à la manière dont nous raisonnons. Découvrons plus précisément le raisonnement inductif et le raisonnement déductif. C’est parti !