 Saviez-vous qu’il est possible de détecter les fraudes comptables, vérifier les résultats électoraux ou encore évaluer la fiabilité d’une source grâce aux mathématiques ? Cette performance s’appuie sur une curiosité statistique fascinante : la loi de Benford. Dans cet épisode, découvrons ce concept étonnant et les applications concrètes que nous pouvons en tirer. C’est parti !
Saviez-vous qu’il est possible de détecter les fraudes comptables, vérifier les résultats électoraux ou encore évaluer la fiabilité d’une source grâce aux mathématiques ? Cette performance s’appuie sur une curiosité statistique fascinante : la loi de Benford. Dans cet épisode, découvrons ce concept étonnant et les applications concrètes que nous pouvons en tirer. C’est parti !
Version vidéo
Version audio
La Loi de Benford
Quelle est cette loi ?
La loi de Benford stipule que dans de nombreuses séries de données issues du monde réel (comme les factures comptables, les mesures naturelles ou les études statistiques) les chiffres ne sont pas répartis de manière uniforme. Contrairement à ce que l’on pourrait croire, les petits chiffres (comme 1 ou 2) apparaissent plus souvent que les grands (comme 8 ou 9). Par exemple :
-
- Environ 30% des nombres commencent par 1
- Moins de 8% commencent par 5
- Moins de 5% commencent par 9
Cette loi est popularisée en 1938 par le physicien Frank Benford. Il recueille 20 000 nombres issus de domaines très variés : tailles de rivières, données démographiques ou encore relevés scientifiques. En les analysant, il constate une régularité frappante dans la fréquence d’apparition des premières décimales. Peu importe le jeu de données, les chiffres apparaissent selon la même répartition statistique.
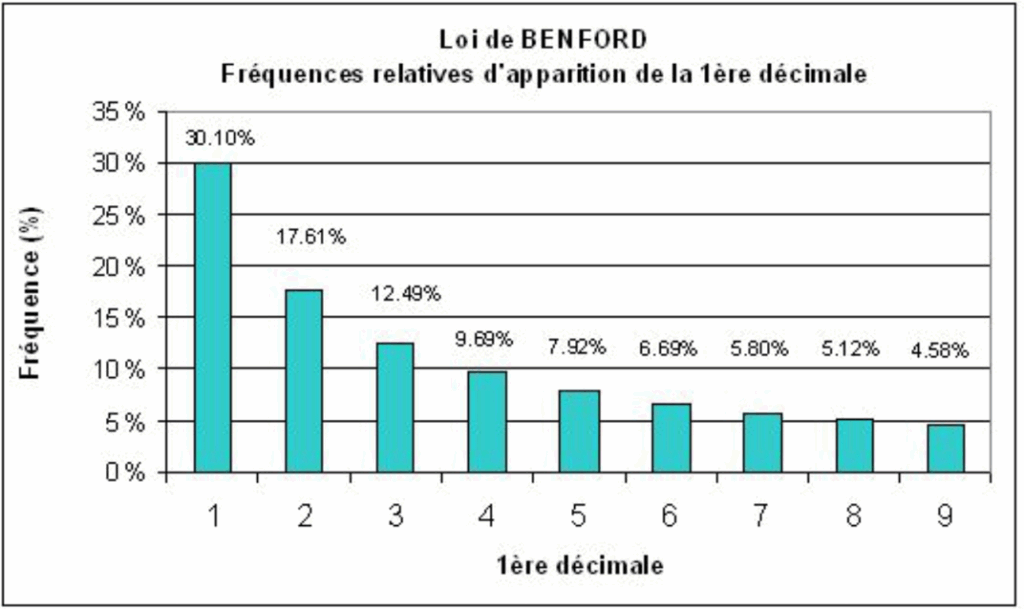
Notons toutefois que la loi de Benford ne s’applique pas à toutes les données. Elle concerne surtout les ensembles de nombres “naturels” qui couvrent plusieurs ordres de grandeur. Les données artificielles, comme des numéros de téléphone ou des codes postaux, ne respectent pas la même fréquence de distribution statistique.
Applications de la loi de Benford
La loi de Benford est un outil mathématique puissant dans de nombreux domaines. Une de ses applications concrètes consiste à l’utiliser pour détecter les fraudes ou falsifications de données.
-
- Des organismes comme l’IRS (le fisc américain) l’utilisent pour traquer les anomalies dans les registres comptables.
- Les statisticiens s’en servent pour analyser les résultats ou les données politiques pour repérer d’éventuelles manipulations.
- L’audit de données massives (big data) à travers le prisme de la loi de Benford permettent de valider l’intégrité de grandes bases de données.
Quoiqu’il en soit, il convient d’éviter les conclusions hâtives. Le fait qu’une source de données dévie de la loi de Benford ne prouve pas qu’elle est obligatoirement fausse. Gardons aussi en tête qu’elle s’applique surtout aux données numériques naturelles comme les prix, les populations ou les mesures physiques.
Avant de conclure, terminons par une réflexion : qu’en est-il du contenu généré par l’intelligence artificielle générative ? Paradoxalement, ChatGPT peut proposer des réponses “artificielles” en s’appuyant sur des données réelles contenues dans ses modèles. Donc, si l’on prend un jeu de données produit par l’IA, suivra-il la répartition statistique de la loi de Benford ? … vous avez 4h !
Conclusion
Utilisée en finance, en science des données ou en criminalistique, la loi de Benford est un outil mathématique puissant. Il repose sur l’observation statistique suivante : dans un jeu de données “naturel”, les chiffres ne sont pas répartis de manière uniforme. Les petits chiffres apparaissent plus souvent que les grands.
Sources
-
- Wikipedia : Loi de Benford : https://fr.wikipedia.org/wiki/Loi_de_Benford
__________________________
Retourner à la page d’accueil du projet P07
__________________________
